Mercedes de la Oliva Fernández - Vie, 26/11/2021 - 09:20

Aprender a interpretar el lenguaje matemático.
Serie: 'Educación en la era digital' (XCII)
El lenguaje matemático, su notación y sus términos precisos, así como su lógica particular, son el fundamento del llamado rigor, que es el que permite que hoy podamos contar con la potencia, fortaleza y validez de los resultados producidos por matemáticos de todos los rincones del planeta, a través de demostraciones formales aceptadas y difundidas.
Ahora bien, ¿La deducción formal y el rigor matemático serán útiles para ser enseñados en la escuela o, será más valioso enseñar y aprender las estrategias del quehacer matemático, tales como trabajar con analogías, encontrar patrones o similitudes, extrapolar problemas a otros contextos, simplificar o generalizar, realizar simulaciones o generar resultados, luego de las comparaciones y del análisis?
A pesar de que estas interrogantes se presentan muy frecuentemente y que los especialistas en didáctica de las matemáticas han reflexionado al respecto, aún persisten autores que defienden el uso del lenguaje formal de esta ciencia, desde los comienzos de la escolaridad, para iniciar el proceso de desarrollo del mencionado rigor matemático tratando, separadamente, la matemática de sus posibles aplicaciones. Esta concepción idealista-platónica ha sido muy utilizada por matemáticos, al considerar que para que el alumno/a pueda por si solo entender las aplicaciones y los problemas que la matemática resuelve, deben conocer a cabalidad y previamente las estructuras básicas de esta ciencia, en forma de enunciados que no requieren demostración (Godino, J., 2004).
Por fortuna, otras concepciones han aparecido a lo largo de los años considerando que debe haber una estrecha relación entre lo que los alumnos conocen y las posibles aplicaciones que la matemática puede ofrecer para la solución de problemas reales. Por supuesto, nos referimos a la concepción constructivista del aprendizaje y del conocimiento.
Según el constructivismo, el conocimiento es activamente construido por el aprendiz. En esta concepción, la cognición es moldeable, por lo que es de utilidad la experiencia del mundo real, así, la realidad existe en función de la construcción mental del que aprende y de la interpretación que del mundo haga, por lo que, aprender es construir y reconstruir esquemas y modelos mentales. En consecuencia, aprender es un proceso individual y colectivo de intercambio, reflexión e interpretación (Castillo, S., 2008).
Entonces, si el aprendizaje en general y, el aprendizaje matemático en particular, es un proceso individual y colectivo de interacción entre el docente y los discentes con el propósito de construir conocimiento, la comunicación, en su concepción más amplia, juega un papel fundamental. Desde este enfoque constructivista, la comunicación que se precisa es aquella que permite la interacción y la negociación de significados entre los participantes en cada sesión de encuentro entre alumnos y docente. Por eso, es importante que el ambiente que se promueva en estos encuentros esté orientado por actividades variadas que permitan que surjan distintas interpretaciones y, así, el espacio donde confluyen alumnos y docente debe entenderse como un foro de discusión en lugar de uno de simple trasmisión de conocimientos (Jiménez, A., Suárez, N., Galindo, S., 2010).
Visto lo anterior y tratando de responder a las preguntas planteadas al inicio, podemos concluir que en la medida en que seamos capaces de manejar un lenguaje matemático básico, a través de una comunicación que facilite los espacios de discusión, intercambio y reflexión; haciendo uso de problemas contextualizados; valorando las opiniones e interpretaciones de todos y, aprendiendo de los errores de forma que podamos reconstruir cuando sea necesario, estaremos más cerca de lograr aprendizajes significativos.
Un paso más: la transferencia
Pero hay un paso más que deben ser capaces de dar nuestros alumnos: la transferencia. Nos referimos a lograr que los aprendizajes obtenidos en las clases de matemáticas puedan ser usados y aplicados, de forma adecuada, en otras asignaturas o incluso en otros contextos fuera de la escuela, de modo que esos conocimientos pasen a formar parte de la cultura de nuestros estudiantes.
Dentro de una concepción moderna de cultura, se reconoce y valora la educación matemática, y no precisamente con el objetivo de formar a nuestros alumnos como matemáticos profesionales, sino formarlos integralmente de modo que sean capaces de comprender, interpretar y valorar, de forma crítica, información y argumentaciones matemáticas que puedan encontrar en diversos contextos, además de ser capaces de discutir o transmitir información matemática que agregue valor para resolver los problemas que se les presenten en la cotidianidad o su vida profesional (Godino, J., 2004).
Hasta ahora, hemos revisado muy brevemente, tres elementos fundamentales en la enseñanza y el aprendizaje de las matemáticas, tal como se muestra en la imagen a continuación: el lenguaje matemático y su característica de valioso código para una comunicación fluida entre alumnos y docente y, entre alumnos; con intercambio permanente en los roles de emisor y receptor de esa comunicación contextualizada; con el propósito de que los aprendizajes alcanzados sean significativos y, así, lograr que puedan transferirse a otros espacios y situaciones.
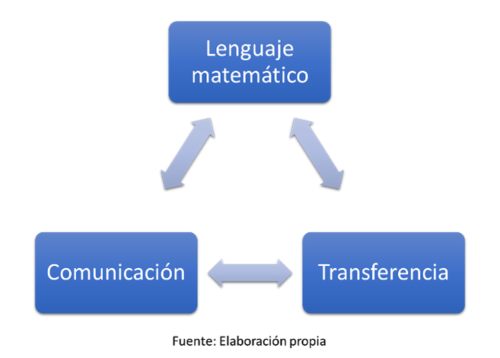
Nos referimos, entonces, a que nuestros/as alumnos puedan hacer uso de los conceptos y estrategias del quehacer matemático, movilizando diversos y variados recursos cognitivos, actitudinales y procedimentales para resolver problemas en diferentes contextos.
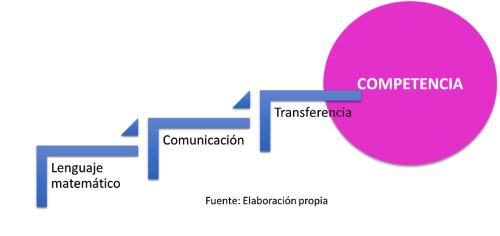
En definitiva, no se trata solamente de conocer el lenguaje y los conceptos matemáticos, es decir, el “saber conocer”; tampoco es suficiente el resolver problemas básicos en el contexto escolar, es decir, el “saber hacer” en espacios limitados; se trata de ir más allá y ser capaces de responder de forma idónea, autónoma, eficaz y con ética, “saber ser”, en diversos y variados contextos (López Gómez, E. 2016).
En otras palabras, nuestro deber como docentes es acompañar a nuestros alumnos, a lo largo de la escolaridad, en el proceso de desarrollo de una de las competencias clave: la competencia matemática.
Referencias bibliográficas:
Castillo, S. (2008): Propuesta pedagógica basada en el constructivismo para el uso óptimo de las TIC en la enseñanza y el aprendizaje de la matemática. Revista Latinoamericana de investigación en matemática educativa. Relime vol.11 no.2. 171-194.
Godino, J. (2004): Didáctica de las Matemáticas para Maestros.
Jiménez, A., Suárez, N., Galindo, S. (2010): La comunicación: Eje en la clase de matemáticas. Praxis & Saber, Revista de Investigación y Pedagogía. Vol 1. Número 2. 173-202.
López Gómez, E. (2016): En torno al concepto de competencia: un análisis de fuentes. Profesorado, Revista de currículum y formación del profesorado. Vol 20. Número 1.
Editor: Universidad Isabel I
Burgos, España
ISSN: 2659-5222


