Solución a los acertijos propuestos en el Día Internacional de las Matemáticas

Persona resolviendo un problema matemático planteado como un juego.

Serie: 'Conectados' (XLIX)

El pasado 14 de marzo fue el Día Internacional de las Matemáticas, una fecha en la que se celebra la importancia de esta disciplina. Para conmemorar este día, decidimos plantear cinco acertijos de distintos niveles de dificultad que han desafiado a los lectores a pensar de manera creativa y utilizar sus habilidades matemáticas para encontrar las soluciones. En esta ocasión, os presentamos las soluciones de estos acertijos, de forma que podáis comparar vuestras respuestas y descubrir si resolvisteis correctamente cada uno de ellos.

Si no sabes de qué acertijos estamos hablando, te recomiendo leer la entrada del blog correspondiente, y poner a prueba tus habilidades antes de comprobar las soluciones.

ACERTIJO 1

Como el estudiante solo puede subir uno o dos peldaños en cada paso. Para llegar al último peldaño, tendrá que hacerlo desde el peldaño número 20 o desde el número 19. De esto se deduce que el número total de formas de subir la escalera completa es la suma del número de formas de subir una escalera de 20 peldaños y del número de formas de subir una escalera de 19 peldaños.

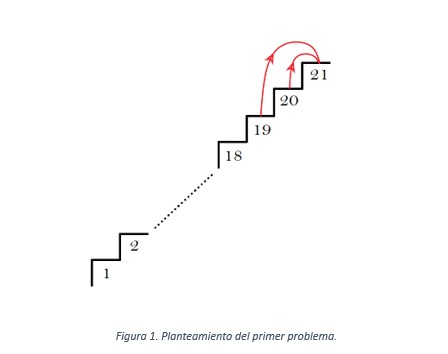
Empezando desde el principio: solo hay una forma de subir una escalera de un único peldaño (1 paso de 1 peldaño) y dos formas de subir una escalera de dos peldaños (2 pasos de 1 peldaño, 1 paso de dos peldaños). El número de formas de subir una escalera de tres peldaños será la suma de los dos valores previos (como se ha argumentado al principio), es decir, 1 + 2 = 3.

De forma recursiva se obtiene la sucesión: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1.597, 2.584, 4.181, 6.765, 10.946, 17.711, …. Cada término de esta sucesión se corresponde con el número de formas de subir una escalera de tantos peldaños como la posición que ocupa. Esta sucesión que quizás te suene es la famosa sucesión de Fibonacci.

Para resolver el problema basta con buscar el elemento número 21 de la sucesión, es decir, 17.711. Como el estudiante acude a clase 199 días al año, podría estar 17.711 / 199 = 89 años sin repetir la forma en la que sube las escaleras ¡Toda una vida!

ACERTIJO 2

Aunque en un primer momento este acertijo pueda parecer irresoluble, tiene una solución tan simple como escurridiza. Para obtener dos montones con el mismo número de caras, basta con hacer un montón de 90 monedas, otro de 10 monedas y voltear todas las monedas del montón pequeño. El motivo por el que funciona es que en el montón de 10 monedas habrá n caras y 10 – n cruces (0≤ n ≤10). Por consiguiente, en el montón de 90 monedas habrá 10 – n caras y 90 – (10 - n) cruces. Es decir, el número de cruces del montón de 10 monedas es igual al número de caras del segundo montón de 90 monedas. Finalmente, si se voltean todas las monedas del montón pequeño, este pasaría a tener 10 – n caras y n cruces.

De forma intuitiva la idea es que las caras que no estén en el montón de 10 monedas deben estar necesariamente en el montón de 90 monedas y esas caras que faltan son necesariamente cruces. Por lo tanto, el número de cruces del montón pequeño es igual al número de cruces del montón grande.

ACERTIJO 3

El primer paso es determinar la cantidad de objetos redondos en ese extraño universo. Del enunciado se deduce que hay: 1 planeta redondo, n alienígenas cuadrados, n ∙ n = n² casas redondas, n ∙ n² = n³ peceras cuadradas y n ∙ n³ = n⁴ peces redondos. Por lo tanto, el número total de objetos redondos es 1 + n² + n⁴. Además, ese número es primo, es decir, sus únicos divisores, son él mismo y la unidad. Para solucionar el problema se factoriza este polinomio en n usando las siguientes identidades notables:

(a + b)² = a² + 2ab + b²,  a²- b² = (a + b) (a - b).

El polinomio se factoriza como sigue:

1 + n² + n⁴ = 1 + n²+ (n²)² = -n² + n² + 1 + n² + (n²)²

= -n² + 1 + 2n² + (n²)² = (1 + n²)² - n²

= (1 + n + n²)(1 - n + n²)

Como 1 + n² + n⁴ es primo, o 1 + n + n² = 1 + n² + n⁴ y 1 - n + n² = 1, o viceversa. En el primer caso, 1 + n² + n⁴ = 1 + n + n² ⇒ n⁴ = n⇒ n³ = 1 ⇒ n = 1. En el segundo caso, 1 + n² + n⁴ = 1 - n + n² ⇒ n⁴ = -n ⇒ n³ = -1 ⇒ n = -1, solución que no tiene sentido en este problema.

Finalmente, se concluye que en este extraño universo hay 3 objetos redondos y 1 alienígena.

ACERTIJO 4

Una solución elegante para este acertijo consiste en considerar el número binario de la posición que ocupa cada grifo. Al haber 100 grifos, serán necesarios 7 dígitos (2⁶ = 64, { 2}⁷ = 128).

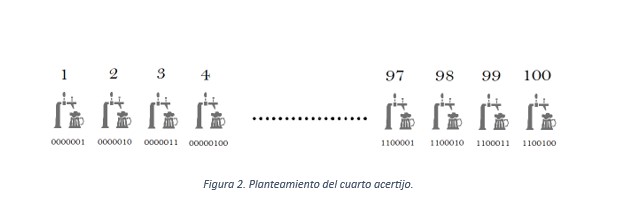
A continuación, se eligen 7 personas y a cada una se le asigna un dígito entre el 1 y el 7 (sin repetir), de forma que cada uno bebe de los grifos donde su dígito sea un 1. Es decir, a la primera de las 7 personas se le asigna el primer dígito y, por lo tanto, bebe de todos los grifos cuya primera cifra sea un 1: 0000001, 0000011, 0000101, 0000111, …. Con las otras 6 personas se procede análogamente.

Es el momento de descubrir qué grifo contiene la cerveza mágica. Para determinar el número en base 2 correspondiente a dicho grifo, el día siguiente a la fiesta se le pregunta a la primera persona si tiene resaca, en caso positivo se coloca un 0 en el primer dígito y en caso negativo un 1. Se hace lo mismo con las otras 6 personas. Por ejemplo, si la primera, la segunda y la sexta personan no tienen resaca, pero la tercera, la cuarta, la quinta y la séptima sí, entonces el grifo sería el 0100011, es decir, el número 35.

Respondiendo a la pregunta del acertijo, para descubrir el grifo que contiene la cerveza mágica tan solo son necesarias 7 personas.

ACERTIJO 5

Este acertijo es quizás el más complicado de los 5. Para solucionarlo se codifican los colores como números: rojo = 0, negro = 1, blanco = 2. La idea es que el último prisionero diga la suma total (menos el suyo) de los sombreros, de forma que el siguiente puede saber el color del suyo restándole a ese número la suma de los que tiene por delante. Si, por ejemplo, la suma de todos los sombreros es 200 y el penúltimo cuenta por delante de él 198, entonces su sombrero ha de ser blanco (200 – 198 = 2 = blanco).

El resto de los prisioneros pueden proceder de forma análoga restándole a la suma total, la suma que tiene por delante y lo que han ido diciendo el resto de los prisioneros que tiene por detrás (excepto el último). Siguiendo con el ejemplo anterior, si el antepenúltimo suma 197 por delante de él, entonces su sombrero ha de ser negro (200 – 197 – 2 = 1 = negro). En el caso del primer prisionero, como no tiene nadie por delante, se puede considerar que las suma de los que tiene por delante es 0. De esta forma se consigue que el procedimiento sea el mismo en todos los casos.

Ahora bien, el último prisionero solo tiene permitido decir uno de los tres colores y en ningún caso la suma total. Para solucionar esta cuestión se puede utilizar la aritmética modular. Para no entrar en formalidades, la aritmética modular funciona como un reloj analógico. Los relojes analógicos tienen 12 horas, pero como el día tiene 24 horas, a las 13 es de nuevo la 1, a las 14 son las 2, …, y las 24 son las 12. En este problema concreto donde solo hay 3 valores, las asignaciones se hacen como en la figura 3:

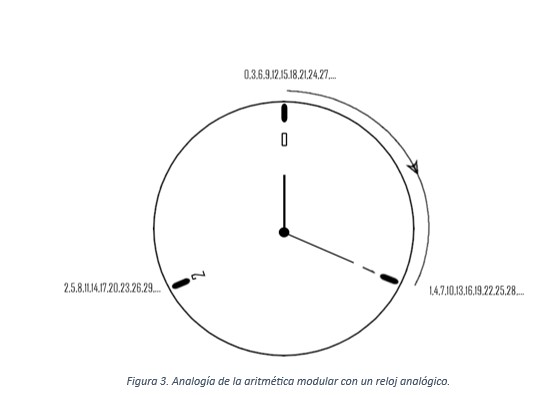
Para números más grandes basta con hacer la división entera entre 3 y tomar el resto, ese resto es el número (0, 1 o 2) al que se le asigna. Por ejemplo 1.234 sería 1 porque 1.234 = 3⋅411 +1, es decir, se dan 411 vueltas completas al reloj y se acaba en el 1.

En resumen, el último prisionero calcula la suma total de los sombreros, le asigna el valor 0, 1 o 2 según se ha explicado y dice en alto el color correspondiente a ese número. El penúltimo prisionero hace el mismo cálculo con los 98 prisioneros siguientes y lo resta del número dicho por el último prisionero. El resto de los prisioneros actúan de la misma forma. Cabe mencionar que el resultado de la resta puede ser -2 y -1. Pensando en la analogía del reloj, los números negativos se corresponderían con dar las vueltas en el sentido contrario al habitual (antihorario). De esta forma, -2 = 1 y  -1=2.

Si todos los prisioneros proceden de esta forma se garantiza que los 99 primeros se salvan. Lamentablemente, el último prisionero solo se salva si tiene la fortuna de que el color de su sombrero coincide con el color asociado a la suma de los 99 primeros sombreros.

Lo más sorprendente de este razonamiento es que permite generalizar la estrategia para cualquier número finito de colores, pudiendo haber incluso más colores que prisioneros. El único inconveniente es que, si los colores se asignan de manera aleatoria, cuantos más colores haya, más difícil será que se salve el último prisionero de la fila.

​Editor: Universidad Isabel I

ISSN 2792-1794

Burgos, España